Động lực của Ủy ban Nobel trong việc quyết định lựa chọn giải thưởng năm nay có lẽ đến từ những tiến bộ ngoạn mục của tính toán lượng tử trong hai thập kỷ qua. Nó có nhiều ứng dụng tiềm năng, từ mật mã đến học máy và truyền thông lượng tử, sử dụng hết sức mạnh mẽ các cặp photon rối và các thực thể liên quan.
Ba nhà khoa học được trao giải Nobel Vật lý 2022 (từ trái qua phải): John Clauser, Anton Zeilinger và Alain Aspect. Nguồn: Quantamagazine
Chúng ta luôn cảm thấy khó chấp nhận một lý thuyết mới, đặc biệt là khi nó chứa nhiều điều trái ngược với trực giác của mình. Lý thuyết cũ thường trở nên quá quen thuộc đến mức chúng ta mặc nhiên chấp nhận nó như là mô tả của “thực tại”. Sự xuất hiện đồng thời của thuyết tương đối hẹp và cơ học lượng tử ở đầu thế kỷ XX là một minh họa hết sức ngoạn mục cho điểm này. Cái phản ứng cố hữu đó của con người đã khởi nguồn cho những cuộc thảo luận bất tận về thực tại, mở màn cho đủ loại giải thích và suy đoán về một bản tính siêu hình học và bản thể học. Nhưng lý thuyết mới cho ta thấy: “Bạn đang nói gì vậy? Thực tại, tồn tại chỉ là những lời sáo rỗng vô nghĩa cũng như những gì tôi nói với bạn. Bạn muốn làm cho chúng bao hàm những ý nghĩa siêu việt, nhưng lại không có cơ sở lập luận vững vàng cho chúng. Hãy thôi đi. Tôi là những gì bạn gọi là thực tại. Vậy thôi”. Với những nỗ lực hết sức có thể, sau nhiều thập kỷ nghiên cứu về các hiện tượng thống trị bởi lý thuyết mới, cuối cùng, các nhà khoa học lại trở nên quen thuộc với lý thuyết mới đến mức họ sẵn sàng chấp nhận nó bất chấp những vi phạm mà nó vẫn tiếp tục gây ra đối với trực giác thông thường của họ. Tuy nhiên, một vài người trong số họ lại không như vậy. Đó là Einstein, người dường như không có vấn đề gì với việc chấp nhận thuyết tương đối (nói một cách nhẹ nhàng là như vậy…) nhưng lại cảm thấy không thoải mái với cơ học lượng tử cho đến khi qua đời vào năm 1955. Năm 1935, cùng với Boris Podolsky và Nathan Rosen, ông đã công bố một bài báo1 thường được gọi là “nghịch lý EPR” [ND: viết tắt từ chữ cái đầu của Einstein, Podolsky và Rosen] với tiêu đề “Mô tả của cơ lượng tử về thực tại vật lý có thể được coi là hoàn chỉnh không?”. Nghịch lý này đã khởi đầu cho nhiều phát triển khởi sắc về cả lý thuyết và thực nghiệm thậm chí cho đến hiện nay. Giải Nobel Vật lý năm 2022 trao cho vế thứ hai, “các thí nghiệm với các photon rối, khẳng định sự vi phạm bất đẳng thức Bell và tiên phong trong khoa học thông tin lượng tử”.
Một sự tấn công lớn của cơ học lượng tử đối với trực giác của chúng ta là tuyên bố một hệ [ND: hệ vật lý] được quan sát nằm trong tập hợp những trạng thái có thể và có thể cũng nằm trong vô số các trạng thái khác. Điều này làm đảo lộn quan niệm của chúng ta về thực tại. Luận điểm này dựa vào các phép đo. Nó cho rằng bất cứ điều gì chúng ta muốn tìm hiểu về hệ đều là kết quả của một phép đo nào đó. Hãy nghĩ về cách chúng ta vẫn nhìn nhận về một hạt. Nếu muốn biết nó ở đâu, chúng ta đo vị trí, x. Hoặc, nếu muốn biết sẽ nó đi đâu, chúng ta đo xung lượng của nó, p. Cơ học lượng tử mô tả các trạng thái có thể có của một hạt như vậy như các vectơ trong một không gian tạo nên từ các trạng thái mà hạt ở đó khi chúng ta thực hiện phép đo. Khi đo x, chúng ta có thể nhận được kết quả x0 và một vectơ cụ thể (x0) mô tả trạng thái của hạt trong trường hợp này. Vì x0 có thể nhận vô số giá trị, nên không gian vectơ của các trạng thái có vô số chiều. Cái này được gọi là không gian Hilbert.
Phát kiến lớn đầu tiên của cơ học lượng tử là phát biểu rằng bất kỳ vectơ nào trong không gian Hilbert đều đại diện cho một trạng thái có thể của hạt, không chỉ các trạng thái (x0) cơ sở của nó. Nói chung, một trạng thái như vậy sẽ là sự chồng chập tuyến tính của các vectơ cơ sở và do đó sẽ có sự trộn lẫn của những vectơ cơ sở. Cơ học lượng tử giải thích điều này bằng cách nói rằng một phép đo trên một trạng thái như vậy có thể cho những kết quả khác nhau, xi, với xác suất được đo bằng các thành phần2 của trạng thái trên các vectơ (xi) cơ sở. Điều này làm cho cơ học lượng tử trở thành một lý thuyết phi tất định; đây là tác động lớn đầu tiên đối với nhận thức của chúng ta.
Phát kiến lớn thứ hai của cơ học lượng tử là giải thích thực tế rằng một số đại lượng không thể đo đồng thời với độ chính xác tùy ý, cái này được gọi là nguyên lý bất định Heisenberg. Để làm được như vậy, nó nói rằng hai đại lượng “không tương thích” liên kết với các vectơ trạng thái của cùng một không gian Hilbert. Trong ví dụ trên, vị trí và xung lượng là những đại lượng không tương thích. Nếu đo xung lượng, chúng ta sẽ nhận được kết quả p0 liên quan đến trạng thái (p0). Nhưng (p0) là một vectơ của cùng một không gian Hilbert phụ thuộc vào các trạng thái (x0). Cụ thể, nó là sự chồng chất tuyến tính của nhiều trạng thái (xi) như vậy và nếu bây giờ chúng ta đo x trên trạng thái đó, chúng ta sẽ đo được một giá trị nào đó với xác suất như nhau. Một trạng thái (x0), với vị trí xác định duy nhất x0, tương ứng với ý tưởng rằng chúng ta có một hạt và một trạng thái (p0), với xung lượng xác định duy nhất p0, tương ứng với ý tưởng về một sóng phẳng. Cơ học lượng tử mô tả theo cách này cái mà chúng ta gọi là lưỡng tính sóng hạt: nói chung, một trạng thái khả dĩ sẽ không mô tả hạt hay sóng rõ ràng, mà là một phiên bản lai của chúng. Nó sẽ giống một hạt hơn nếu các thành phần của nó trên cơ sở (x0) liên quan đến ít vectơ cơ sở hơn và giống như một sóng hơn nếu các thành phần của nó trên cơ sở (p0) bao gồm ít vectơ cơ sở hơn. Để một trạng thái trông giống càng nhiều càng tốt so với những gì mà chúng ta vẫn quen dùng, nó cần liên quan đến ít thành phần trên cả hai cơ sở (x0) và (p0): người ta nói về một “bó sóng”. Thông thường, các thành phần của nó trên (x) được coi là có phân bố Gauss xung quanh x0 với độ rộng Dx và các thành phần của nó trên (p) được coi là có phân bố Gauss xung quanh p0 với độ rộng Dp. Hệ thức bất định Heisenberg cho chúng ta biết rằng tích Dp×Dx phải lớn hơn hằng số Planck, h = 6,6 10–34 Jun.giây, một hằng số cơ bản của vật lý lượng tử đo mức độ không tương thích giữa các đại lượng x và p.

John Bell tại văn phòng ở CERN của mình.
Trong cách giải thích chính thống của cơ học lượng tử, chúng ta chỉ quan tâm đến những gì có thể đo được và không có tham vọng đưa ra cách giải thích không cần thiết về các trạng thái khác ngoài cơ sở liên quan đến phép đo. Chúng ta sử dụng chúng để mô tả một hệ, nhưng lý do duy nhất khi áp dụng mô tả này là do nó hoạt động hết sức tuyệt vời, cho phép chúng ta xây dựng nên một lý thuyết tao nhã về tất cả các hiện tượng quan sát được ở quy mô nguyên tử và nhỏ hơn. Thay vào đó, những cách giải thích không chính thống của cơ học lượng tử, với động lực bác bỏ sự phi tất định của nó, dành nhiều sự chú ý cho những cách giải thích có thể có về trạng thái tổng quát nhất của không gian Hilbert. Điển hình của điều sau là cách giải thích khó hiểu được đưa ra bởi nghịch lý EPR. Nó xem xét việc đo p tại một điểm A trong không gian, đối với một hệ ở trạng thái khác với trạng thái của hệ cơ sở (p); nhận được kết quả là p0, và hệ nằm ở trạng thái (p0). Trước khi thực hiện phép đo, có thể có nhiều kết quả khác, với các xác suất được đo bằng các thành phần của trạng thái trên cơ sở (p). Đồng thời với phép đo này, người ta đo p tại một điểm B, cách xa A. Làm sao B biết được kết quả của phép đo ở A? Làm thế nào nó có thể biết rằng hệ nằm ở trạng thái (p0) và kết quả của phép đo của nó phải là p0? Thông tin từ A đến B cần phải truyền đi ngay lập tức, mà điều này lại vi phạm thuyết tương đối hẹp; người ta nói về tính “phi định xứ”. Cách giải thích phi chính thống như vậy, coi phép đo gây ra cái mà người ta gọi là “suy sụp” của trạng thái ban đầu thành trạng thái được đo và sự suy sụp đó phải là phi định xứ.
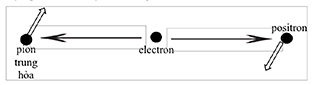
Nghịch lý EPR được David Bohm3 phát biểu lại vào năm 1951 dưới một hình thức hấp dẫn trực giác hơn. Nó xem xét một cặp hạt được tạo ra cùng nhau từ một hạt mẹ, theo cách mà các đặc tính của chúng có tương quan với nhau. Một ví dụ cụ thể là một cặp photon, hoặc tương đương là một cặp electron-positron, được tạo ra từ sự phân rã của hạt có spin bằng không (hạt vô hướng), chẳng hạn như pion trung hòa, và bay ra xa nhau. Các hạt phân rã có spin, có thể đo được và được tìm thấy ở hai trạng thái khả dĩ, được gọi là “spin-lên” và “spin-xuống”. Phép đo như vậy ngụ ý chọn một trục theo đó spin được đo. Việc chọn một trục khác cũng cho ra hai kết quả, lên hoặc xuống, nhưng trạng thái spin-lên mới bây giờ là sự chồng chập của các trạng thái spin-lên và spin-xuống thu được liên quan đến phép đo sử dụng trục đầu tiên. Và cũng tương tự cho trạng thái spin-xuống mới. Vì hạt mẹ có spin bằng không, các hạt phân rã phải có spin ngược chiều nhau. Cơ học lượng tử mô tả cặp hạt phân rã là một trạng thái đơn lẻ, về mặt spin, nằm trong không gian Hilbert hai chiều phụ thuộc vào các trạng thái (lên, xuống) và (xuống, lên). Ở trạng thái (lên, xuống), hạt bên trái có spin hướng lên và hạt bên phải có spin hướng xuống; và tương tự cho trạng thái (xuống, lên). Không thể có trạng thái (lên, lên) và (xuống, xuống) trong mô tả như vậy: người nói rằng các hạt phân rã bị “rối” trong một trạng thái chung và người ta nói về “sự rối”. Trong trường hợp như vậy, nghịch lý EPR có dạng sau: người ta đo spin của hạt bên trái và tìm ra kết quả spin của hạt bên phải buộc phải có, ở trạng thái xác định rõ. Sẽ không có gì sai với điều này nếu chúng ta giải thích trạng thái của cặp hạt là ở một trong các trạng thái (lên, xuống) hoặc (xuống, lên) trước khi đo. Nhưng nếu chúng ta giải thích trạng thái ban đầu của cặp hạt là sự suy sụp thành một trong hai trạng thái khả dĩ chỉ sau khi thực hiện phép đo, thì người ta phải đối mặt với vấn đề phi định xứ: làm sao hạt ở phía bên phải có thể biết được kết quả của phép đo thực hiện với hạt bên trái? Cách giải thích chính thống của cơ học lượng tử không có vấn đề gì với câu đố rõ ràng này, nó không cần phải tuyên bố rằng trạng thái rối sụp đổ ngay lập tức ở mọi nơi bởi vì nó chỉ quan tâm đến các trạng thái được đo.

Trung Quốc đã vận hành thành công vệ tinh Mặc Tử cung cấp các cặp photon rối vào năm 2017 tới các trạm mặt đất gần Vienna và Bắc Kinh, cách nhau 7.400 km.
Một bước tiến quan trọng sau đó đã được thực hiện vào năm 1964 bởi John Bell tại CERN với một định lý được đặt theo tên ông4. Bell là một người đàn ông hết sức khiêm nhường và lôi cuốn, thật đáng buồn ông lại mất sớm. Tôi nhớ ông đã tổ chức một cuộc hội thảo về định lý của mình vào năm 1965 và giảng cho chúng tôi về vi phạm đối xứng CP với phân rã K0 tại một trường học mùa hè ở Les Houches cùng năm này. Ở thời điểm đó, cơ học lượng tử gần như đã được cộng đồng vật lý chấp nhận nhưng các cuộc thảo luận về cách lý giải nó sao cho ít trái với trực giác thông thường nhất vẫn tiếp tục diễn ra. Những cuộc trao đổi đó là nguồn cơn của nhiều ý tưởng thú vị. Trong số đó có những lý thuyết như lý thuyết biến ẩn5. Trong khuôn khổ bài viết này, chúng ta sẽ không bàn về những lý thuyết như vậy để tránh đi quá xa. Có thể khẳng định rằng mối quan tâm chính của những người đặt vấn đề về cách giải thích chính thống của cơ học lượng tử, cái gọi là cách giải thích Copenhagen, là phủ nhận tính phi tất định của nó, bác bỏ sự tồn tại các trạng thái của một hệ trong đó các giá trị được lấy bởi một số đại lượng mô tả tính chất của nó không được xác định một cách chính xác và duy nhất. Định lý Bell nhằm mục đích phân biệt cơ học lượng tử chính thống và một loạt lý thuyết tất định. Ví dụ về sự phân rã của hạt có spin bằng không cho thấy rằng không thể tạo ra mối tương quan giữa các phép đo thực hiện ở bên trái và bên phải mạnh như với cơ học lượng tử. Ở dạng đơn giản, nó có thể được mô tả như sau: thành phần spin của hạt bên trái được đo dọc theo một trong hai trục, vuông góc với nhau và vuông góc với đường bay, kí hiệu 1 và 2. Thành phần spin của hạt bên phải được đo trên một trong các trục 3 và 4 là đường phân giác của trục 1 và 2. Người ta quyết định theo ý mình, đối với mỗi phân rã, Sz1 hoặc Sz2 được đo ở phía bên trái và, một cách độc lập, Sz3 hoặc Sz4 được đo ở phía bên phải. Sau đó, đối với loại lý thuyết tất định được Bell xem xét, khi tính trung bình trên một số lượng lớn các phép đo (với <SziSzj> là giá trị trung bình của tích SziSzj), <Sz1Sz3> + <Sz1Sz4> + <Sz2Sz3> – <Sz2Sz4> không được vượt quá 1/2: đây là bất đẳng thức Bell; ngược lại giá trị cơ lượng tử của cùng một đại lượng là 1/√2 với hệ số √2 lớn hơn giá trị xác định lớn nhất có thể. Như vậy sự vi phạm bất đẳng thức Bell là một đặc điểm khác biệt của cơ học lượng tử.
Giải Nobel Vật lý 2022 trao thưởng cho ba thí nghiệm điển hình đưa ra bằng chứng về vi phạm bất đẳng thức Bell.
“Nghịch lý EPR” đã khởi đầu cho một loạt các phát triển về cả lý thuyết và thực nghiệm vẫn còn tồn tại cho đến ngày nay. Giải Nobel Vật lý năm 2022 trao cho vế thứ hai, “các thí nghiệm với các photon rối, khẳng định sự vi phạm bất đẳng thức Bell và tiên phong trong khoa học thông tin lượng tử”.
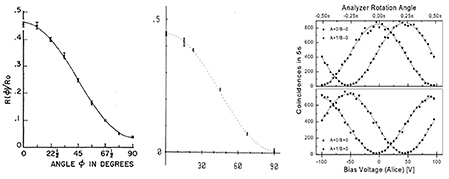
Năm 1972, John Clauser cùng với Stuart Freedman (mất năm 2012) đã công bố bằng chứng thực nghiệm đầu tiên về vi phạm bất đẳng thức Bell6. Thí nghiệm được thực hiện tại Phòng thí nghiệm Lawrence ở Berkeley, quan sát sự phân rã của một nguyên tử canxi từ trạng thái có tổng mômen động lượng J = 0 đến trạng thái J = 1 thông qua photon thứ nhất γ1 có bước sóng 5513 Å, tiếp theo là phân rã đến trạng thái J = 0 thông qua photon thứ hai γ2 có bước sóng 4227 Å. Hai photon được quan sát đồng thời (kĩ thuật trùng phùng), trạng thái J = 1 có thời gian sống chỉ ~5 ns, sau khi đi qua các thiết bị phân cực tuyến tính. Kết quả thu được hoàn toàn phù hợp với cơ học lượng tử và đưa ra bằng chứng về sự vi phạm bất đẳng thức Bell với độ tin cậy hơn 6 độ lệch chuẩn [ND: trong thống kế 3 độ lệch chuẩn tương đương với mức độ tin cậy 99,7%]. Trong thí nghiệm này, trạng thái J = 1 của nguyên tử canxi đóng vai trò hạt mẹ có spin bằng không trong thí nghiệm Bohm gây ra sự rối của cặp photon γ1+γ2.
Từ năm 1980 đến năm 1982, Alain Aspect, cùng với J. Dalibard, P. Grangier và G.Roger đã lặp lại thí nghiệm Freedman-Clauser tại Viện Quang học, Orsay (Pháp), cải thiện đáng kể một số tính năng kỹ thuật khi thiết lập thí nghiệm, bao gồm cả laser được sử dụng để kích thích các nguyên tử canxi về trạng thái J = 0 ban đầu và các bộ phân cực được cải tiến với các cài đặt để có thể thay đổi trong một khoảng thời gian ngắn. Một lần nữa, nhóm nghiên cứu thu được bằng chứng rõ ràng về vi phạm các bất đẳng thức Bell7 (5 độ lệch chuẩn). Cải tiến chính của thí nghiệm này so với thí nghiệm Freedman-Clauser là độ tin cậy của kết quả đo.
Phiên bản thứ ba của thí nghiệm Freedman-Clauser được công bố vào năm 19988 bởi nhóm của Anton Zeilinger tại Viện Vật lý Thực nghiệm của Đại học Innsbruck với cách thiết lập thí nghiệm hoàn toàn khác (cặp photon rối được tạo ra bằng cách bơm tinh thể Beta-Baryum-Borate với ánh sáng laser iôn argon). Lần này, bất đẳng thức Bell đã bị vi phạm với hơn 30 độ lệch chuẩn và quan trọng hơn, điều kiện định xứ, nghĩa là phép đo ở phía trái không có thời gian để cho phép đo ở phía phải biết về cài đặt của máy phân tích của nó, đã hoàn toàn được thực thi với các phát hiện photon cách nhau ~400 m (1,33 μs với vận tốc ánh sáng), siêu nhanh (<30 ns), máy phân tích được cài đặt ngẫu nhiên, và ghi nhận dữ liệu hoàn toàn độc lập.
Ngày nay, một loạt các kết quả thực nghiệm mới cũng đã chứng minh sự vi phạm bất đẳng thức Bell ủng hộ cách giải thích chính thống của cơ học lượng tử với độ chính xác chưa từng có. Trong bối cảnh như vậy, thật hết sức cám dỗ để cơ học lượng tử và cách giải thích chính thống có thể tuyên bố chiến thắng vang dội và làm nín lặng những tiếng nói đòi hỏi diễn giải cơ học lượng tử dùng logic “vĩ mô”. Tuy nhiên, sự kiêu ngạo như vậy sẽ không phù hợp bởi nó bỏ qua thực tế rằng cơ học lượng tử và thuyết tương đối rộng không tương thích ở thang Planck. Điều này vốn được dịch bằng một ngôn ngữ không chính xác về mặt chính trị, có nghĩa là ít nhất một trong hai thuyết này và rất có thể cả hai đều sai. Nó cũng sẽ bỏ qua những ý tưởng phong phú truyền cảm hứng bởi nền tảng cơ học lượng tử như ý tưởng được Gerard ‘t Hooft9 xem xét gần đây. Nổi bật trong số này là phỏng đoán ER = EPR10, đề xuất bởi Leonard Susskind và Juan Maldacena năm 2013, gợi ý rằng việc xem xét một cặp lỗ đen rối có thể đem lại cơ sở để thống nhất cơ học lượng tử và thuyết tương đối.
Động lực của Ủy ban Nobel trong việc quyết định lựa chọn giải thưởng năm nay có lẽ đến từ những tiến bộ ngoạn mục của tính toán lượng tử trong hai thập kỷ qua.
Trước khi kết thúc bài viết này, tôi phải nói rằng động lực của Ủy ban Nobel trong việc quyết định lựa chọn giải thưởng năm nay có lẽ đến từ những tiến bộ ngoạn mục của tính toán lượng tử trong hai thập kỷ qua. Tính toán lượng tử có nhiều ứng dụng tiềm năng, từ mật mã đến học máy và truyền thông lượng tử, sử dụng hết sức với tần suất cao các cặp photon rối và các thực thể liên quan. Trung Quốc đã phát triển mạng lưới Phân phối Khóa Lượng tử lớn nhất thế giới giữa Bắc Kinh và Thượng Hải và đã vận hành thành công vệ tinh Micius cung cấp các cặp photon rối vào năm 2017 tới các trạm mặt đất gần Vienna và Bắc Kinh, cách nhau khoảng 7.400 km. Các cặp photon rối này có thể được sử dụng làm khóa mã hóa, giúp cho việc giao tiếp giữa hai đối tác có thể được giữ bí mật khỏi các hacker, hiệu quả hơn nhiều so với trước đây.
Thật thú vị khi nhận xét rằng ba nhà khoa học, với lý tưởng phổ biến kiến thức tới công chúng càng rộng rãi càng tốt, hiện lại đang được khen thưởng vì đã đi tiên phong trong nỗ lực giữ bí mật thông tin cao nhất có thể… tôi chỉ đang nói đùa thôi.□
—-
Chú thích
1 Einstein, A., Podolsky, B. and Rosen, N., 1935, Phys. Rev. 47 10 777. https://en.wikipedia.org/wiki/EPR_paradox. Như một lời khuyên chung cho người đọc không quen thuộc với các vấn đề được thảo luận trong bài viết này, tôi khuyên các bạn nên đọc các bài viết trên Wikipedia, tất cả đều có chất lượng tốt, khi duyệt web để tìm thông tin về các vấn đề đó. Thật vậy, nhiều bài báo khác trộn lẫn khoa học cấp thấp với triết học cấp thấp, tạo nên sự bối rối trong tâm trí người đọc.
2 Trên thực tế, bình phương mô đun của các thành phần, là số phức, nhưng thảo luận hiện tại bỏ qua điều này.
3 Bohm, D., 1951, Quantum Theory, Prentice-Hall, Englewood Cliffs. https://en.wikipedia.org/wiki/EPR_paradox.
4 https://en.wikipedia.org/wiki/Bell%27s_theorem
5 https://en.wikipedia.org/wiki/Hidden-variable_theory
6 Freedman, S.J. and Clauser, J.F., 1972, Experimental test of local hidden-variable theories, Phys. Rev. Lett., 28/14, 938.
7 Aspect, A., Grangier, P. and Roger, G., 1981, Phys. Rev. Lett., 47, 460. Aspect, A., Grangier, P. and Roger, G., 1982, Phys. Rev. Lett., 49, 91. Aspect, A., Dalibard, J. and Roger, G., 1982, Experimental Test of Bell’s Inequalities Using Time-Varying Analyzers, Phys. Rev. Lett., 49, 1804.
8 Weihs, G., Jennewein, T., Simon, C., Weinfurter, H. and Zeilinger, A., 1998, Violation of Bell’s Inequality under Strict Einstein Locality Conditions, Phys. Rev. Lett. 81/23 5039
9 ‘t Hooft, 2016, The cellular automaton interpretation of quantum mechanics, Fondamental theories of physics, Volume 84, Springer
10 Maldacena, J. and Susskind, L., 2013, Cool horizons for entangled black holes, Fortschr. Phys., 61/9, 781;
https://en.wikipedia.org/wiki/ER_%3D_EPR





giải thưởng này rất giá trị
Trả lờiXóa